A LOW-COST SINGLE-ENDED TRIODE AMPLIFIER
by Fred Nachbaur, Dogstar Music ©2002
2: HOW IT WORKS
As mentioned, and as you've probably noticed from the picture, this project uses just one
tube. However, the tube chosen (13EM7) actually contains two separate triode structures.
One is physically quite small, and is capable of a large signal gain but little power. It
therefore makes an ideal preamplifier stage. The other section is larger, and has a lower
voltage gain, but is capable of a significant amount of current. It therefore can deliver
up to about two watts of power into a speaker load under the appropriate conditions.
This tube was originally designed to be used in television sets. The small, high-gain
section was typically used as the vertical oscillator, and the larger section as the
vertical output stage. However, it also makes a splendid audio tube. If you think about
it, linearity is no less critical in television sets than it is in high-fidelity audio.
At the same time, there isn't the "mystique" around television tubes that there
is around so-called "audio" devices, so the price is a lot more reasonable
than otherwise quite similar tubes such as, say, the Type 45.
There are a few different variants of this tube which can be used. The 13EM7/15EA7 is
functionally identical to the plain 13EM7. If you're buying a tube for this project,
either variant will be fine. If you have a "junk box" of tubes, but don't have
a 13EM7, you might have a look to see if you can find a 10EM7. This is the same tube, but
with a lower-voltage filament. It can be used in this design if a filament dropping
resistor is added (details later). The 6EM7 or 6EM7/6EA7 could conceivably be used also,
but will be a bit more involved; for this reason this option is suggested only for more
experienced tube equipment builders. Similarly, there are other tubes such as 13FM7 which
would work in this kind of circuit, but would require the harder-to-find 12-pin
"compactron" socket, whereas the *EM7 series takes the more common
"octal" socket.
A schematic diagram is shown below, and a detailed circuit explanation follows:
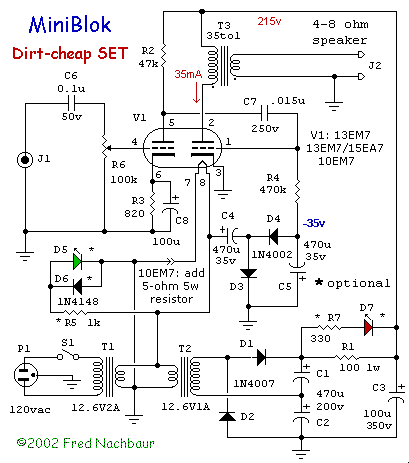
1: POWER SUPPLY
There are essentially three separate power supplies required, as suggested by the three
battery symbols in the basic common-cathode amplifier circuit on the previous page. The
first (usually called the "A" supply) is to heat the filament of the tube, the
second provides the high voltage for the plate circuits (the "B" supply), and
the third provides the negative grid bias for the power amplifier ("C" supply).
Incoming power from the 120 VAC power line is switched by on-off switch S1, and thence
applied to step-down transformer T1. This is rated at 12.6 volts at 2 amperes, and in
practise will supply very close to 13 volts at its secondary. This is what heats the
tube's filament. Note that we don't bother converting to DC, in this application an AC
heater is just fine because 1) we're not dealing with extremely high gain, and 2) the
13EM7's indirectly-heated cathode is naturally highly immune to AC hum.
At the same time, this 13 volt AC supply is connected to the network consisting of diodes
D3 and D4, and capacitors C4 and C5. This is a "voltage doubler" circuit. During
positive half-cycles, C4 is charged up to the peak value of the incoming AC voltage (about
13 volts times 1.4, or 18 volts). During negative half-cycles, this charged capacitor is
essentially placed in series with the incoming supply, causing capacitor C5 to about
twice the peak value after only a few cycles. This forms our -35 volt grid bias supply.
An optional pilot lamp network consisting of LED (light-emitting diode) D5, resistor R5,
and diode D6 can be also connected to the 13 volt line. Resistor R5 limits the maximum
current to a safe level for the LED, and D6 prevents excessive reverse voltage during
negative half-cycles.
Finally, the secondary of T1 is also connected to the low-voltage winding of a similar
transformer T2 (12.6 volts at 1 ampere). T2 steps the 13 volts back up to approximately
110 volts AC. From there, another voltage doubler (this time with a slightly different
topology) generates the high-voltage DC required by the plate circuits. During positive
half-cycles, capacitor C1 is charged via diode D1; and during negative half-cycles,
capacitor C2 is charged via diode D2. Since these two capacitors are essentially in
series, the net voltage across them will be close to twice the peak value of the incoming
AC.
You may notice that the size of the tank capacitors is quite large (470 µF), especially
for such a little amplifier. This is necessary to keep hum to acceptable levels; one of the
drawbacks of the single-ended triode design is that it is quite sensitive to ripple on the
supply line. Also, the schematic shows these with a 200 volt rating, whereas the parts list
specifies a 160 volt minimum. This is because I used capacitors salvaged from computer power
supplies, which typically have the 200 volt rating.
Resistor R1 and capacitor C3 provide additional "smoothing" or
"filtering" to reduce the amount of ripple on the DC supply. This is needed
to reduce the amplifier's hum level to an acceptable level. A side effect is that there
is some voltage loss (drop) across resistor R1, due to the current flowing through it.
The net effect of this loss plus transformer losses is that the final voltage appearing
at the output of the B power supply is approximately 215 volts during normal operation.
Another optional pilot lamp consisting of resistor R7 and LED D7 senses this voltage
drop across R1. It's neat to watch this in operation; on power-up, it flashes briefly
while the capacitors charge and there is a net current into capacitor C3. It then goes
out while the tube heats up and there is not yet any current draw. Once the filament
reaches operating temperature, the plate circuits begin to draw current and the lamp
starts to glow. Again, resistor R7 limits the amount of current that is allowed to pass
through the LED.
I should mention that the amplifier's total hum content could be reduced by adding another
stage of ripple filtration for the preamplifier stage. However, I didn't find the difference
significant enough to warrant the additional parts.
2: PREAMPLIFIER
The preamplifier stage consists of only five electrical parts in addition to the tube!
The schematic diagram is repeated below for convenience.

The incoming signal from input jack J1 passes through blocking capacitor C6 to the grid
of the preamplifier stage. This capacitor prevents any DC voltage that might be riding
on our input signal from being applied to the grid, and causing its operating point to
shift. It also blocks unwanted very low frequencies (below about 16 Hz.) from passing
to the amplifier.
R6 is our volume control. Notice that it also provides a DC return path to common ground
for the preamplifier grid. This assures that the voltage on the grid is close to zero
volts.
Note also that there is a resistor, R3, in series with the cathode. This indirectly
provides the necessary grid bias. Here's how that works: current through the tube
also passes through the resistor, creating a voltage drop. The value of the resistor is
chosen such that about 2 milliamperes flowing through the cathode causes a 1.5 volt
drop. This causes the voltage on the cathode to be positive with respect to ground
(0 volts) by about 1.5 volts. Since the grid is at ground potential, it follows that it
will be 1.5 volts negative with respect to the cathode.
This biasing approach also has a self-adjusting effect; if the average current should
increase, the bias voltage increases, tending to cause the current to
decrease. This describes a "negative feedback" system, helping to
stabilize the preamplifier. Note, however, that this would also introduce negative
feedback for AC signals also. Since the purpose of this exercise is to build an amplifier
with no externally applied feedback, we add capacitor C8. This essentially negates any
feedback for AC (signal) voltages by acting as a "bypass".
Resistor R2 provides the plate circuit load for the preamp. As the plate current changes
with incoming signal, the voltage drop across R2 changes in step. As it works out, a
one-volt change at the grid will result in about a 35 volt change at the plate -- in
other words, the circuit gives us a voltage gain of about 35.
3: POWER AMPLIFIER
The power amplifier stage is even simpler yet!

The required grid bias for the power amplifier stage is approximately 35 volts. If we
used the same cathode-bias approach as for the preamplifier, this 35 volts would
effectively subtract from our plate supply, greatly reducing our available output power.
Mainly for this reason we use a "fixed bias" approach for the power amp,
employing a separate "C" supply to provide the bias. This bias voltage is
applied to the grid of the power amp via resistor R4.
Blocking capacitor C7 (also called a "coupling capacitor") allows the
preamplified AC signal to pass from the plate of the preamp to the grid of the power amp,
while blocking the DC difference between these two points (over +100 volts on the plate
of the preamp, and -35 volts on the grid of the power amp).
Finally, the plate current of the power amp is allowed to flow through the primary
winding of output transformer T3. This is necessary because tubes typically have a high
output voltage swing, but low current capability. Another way of putting this is that
they have a "high output resistance". The transformer acts as a voltage
step-down and current step-up device, matching the low-resistance speaker load to the
high-resistance amplifier output resistance. (There are ways of building tube amps
without output transformers, but they tend to be rather complex, inefficient, and often
unstable. Definitely only for more advanced and adventurous designers and experimenters!)
The secondary of the output transformer is connected to the speaker -- and our amplifier
is complete! As shown, the amplifier's output resistance (after the transformer) is on the
order of about 6 ohms. It will therefore work fine with either 8-ohm or 4-ohm speaker
loads. Distortion will be marginally less when using 8-ohm speaker loads, however.
4: (ADVANCED)
Operating Points and Load Lines
This section will mainly be of interest to more advanced readers, but might be worth a look-over
if you're interested in the design procedure that went into this little project.
A: Power amplifier
An important design decision is the choice of operating points of the various amplifier stages.
Of particular interest is the operating point of the final power stage. For the MiniBlok amplifier,
I decided to set the operating point to give a quiescent plate dissipation of about 7.5 watts, or
about 3/4 of the tube's maximum rated dissipation of 10 watts. The graph below shows my chosen
operating point (about 210 volts at 35 mA) in blue, plotted on the plate curves for the power
triode section of the *EM7.
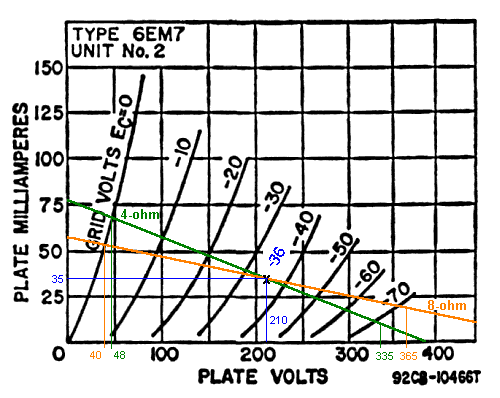
After defining the operating point, I plotted the load line for the 35:1 turns ratio output
transformer for both an 8-ohm and a 4-ohm secondary load. For the 8-ohm load, the reflected
primary load resistance is (35 * 35 * 8) = 9800 ohms; the 9800 ohm loadline is shown in orange.
Similarly, for a 4-ohm load, the reflected primary load resistance will be (35 * 35 * 4) = 4900
ohms. This loadline is shown in green. [If you're wondering how I came up with these lines, the
key is that the load impedance dictates the slope of the line. If you divide the x-intercept of
the green line (about 380 volts) by the y-intercept (about 78 mA) you come up with about 4900
ohms.] Both loadlines have to pass through the operating point, of course, since that is our
quiescent (no signal) operating point.
The loadlines can give us an idea of the maximum possible performance that can be expected from
the amplifier. Starting with the 8-ohm loadline, the furthest that the tube can go to the left
would be where the loadline intersects the grid voltage = 0 point, since beyond that it would
rapidly clip. So this means that our maximum unclipped peak signal voltage would be about 36 volts.
At the other extreme, such a signal on the grid would cause it to reach (-36 * 2) = -72 volts.
These two extremes represent plate voltages of 40 and 365 volts, respectively, or a total
peak-to-peak swing of 325 volts. Dividing by 2.828 (ratio of peak-to-peak to RMS) gives us a
maximum RMS voltage of 115 volts. Squaring and dividing by 9800 ohms load resistance gives us a
maximum undistored output power of 1.35 watts.
Similarly, we can compute that with a 4-ohm load, the theoretical maximum attainable output power
will be on the order of 2.1 watts.
Why the disparity between predicted and measured output power? Mainly this is because of losses
in the output transformer. DC resistance of the windings, hysteresis and eddy current losses, and
the fact that an air-gap is needed for single-ended amplifiers, all contribute to the losses. Note
that the losses are proportionally more at lower load impedance, due to the increased current that
flows in both the primary and the secondary of the transformer. It should, however, be pointed out
that the presence of the air-gap greatly extends the transformer's low-frequency response; even
with the little wee transformer I used, the 3 dB corner is way down at 40 Hz.!
Note also that a significantly higher output power is attainable with a lower value of plate load.
However, this needs to be balanced with distortion. Take a look at the 4-ohm loadline (green).
Compare the length of the line segment between grid voltages 0 and -10 volts, with the length of
the segment between -60 and -70 volts. In a linear system, these line segments lengths would be
identical. Note, however, that the segment on the right (near cutoff) side is quite a bit shorter
than the one on the left (near saturation). The difference between these lengths represents the
amount of non-linearity in the amplifiers.
Now look at the 8-ohm loadline (orange line). You'll readily see that the difference between the
lengths of the two comparable line segments is considerably less. The line segment between 0 and
-10 volts is somewhat shorter, and the one between -60 and -70 is somewhat longer. In other words,
even though we can get less usable power at higher load resistances, our linearity improves (and
therefore, total distortion decreases).
B: Voltage amplifier
The voltage amplifier is a bit more straight-forward, since the plate load is almost the same for
DC as it is for AC. The operating point was first chosen, based on the maximum plate dissipation
(1.5 watts) and the requirement for at least 36 volts of linear operation in either direction.
The chosen point of approximately 140 volts plate voltage and 1.7 mA satisfies the dissipation
requirement handily (0.24 watts). Let's see how it does on the voltage swing issue.
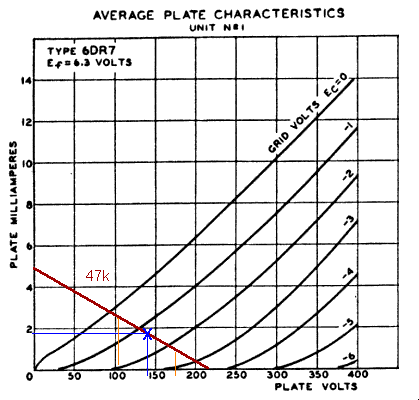
Given a 220 volt supply and 1.7 mA quiescent current, the required plate load resistor is
(220 - 140) / 1.7 = 47k. So we draw the load line (in red) from the supply voltage (x-axis
intercept) to the "short-circuit current", or supply voltage divided by load resistance
(y-axis intercept). Looking it over, we find that plate voltage can travel almost to the supply
voltage (positive excursion of 220 - 140 = 80 volts), or down to about 90 volts (negative
excursion = 140 - 90 = 50 volts) where the loadline intercepts the grid voltage = 0 curve. So
there should be plenty of drive available.
There's just one other factor that needs to be taken into account; the effect of the power amp's
grid resistor. This essentially is in parallel with the plate load resistor as far as AC signal
is concerned. So for AC, the load resistance is actually on the order of 42.7k. One way of dealing
with this is to draw a second load line, whose slope is the net AC load resistance, and which
passes through the operating point.
However, in this case the difference is so slight that the graphical approach is virtually useless;
the two lines would be too close together to readily discern the difference. So in a case like this
it's easier (and probably more accurate) to simply estimate a 9 percent reduction in voltage
swing, since the difference between the DC load (47k) and the AC load (42.7k) is about 9 percent.
This yields a positive and negative maximum of 72 volts and 45 volts respectively, well above our
36 volt requirement.
Looking at our load line we can also approximate the gain of the stage that we can expect. Go along
the loadline in either direction, to a point where the grid voltage is one volt higher or lower, and
drop a line to the horizontal axis (these points are shown with orange lines in the diagram). We
see that a one volt change on the grid results in about a 35 volt change on the plate. Again
deducting 9 percent to account for the PA grid resistor, that comes to about 32 volts. So, for a
full 36 volt swing, we would need about 1.1 volts on the grid. Since our grid bias is a few tenths
of a volt in excess of this, we can rest assured that we'll get full output from the amplifier,
without having the preamp grid ever go positive.
A final note - in this analysis there is no need to account for the effect of the cathode resistor.
This is because for DC the drop across it is so low (1.3 volts) compared to the plate supply, and
for AC it is effectively bypassed by a large capacitor.








